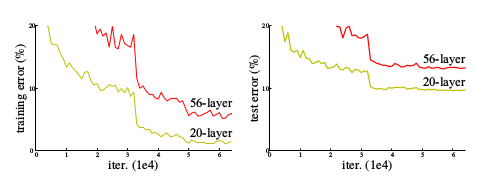
网络在堆叠到越来越深之后,由于BP算法所依赖的链式法则的连乘形式,会出现梯度消失和梯度下降的问题。初始标准化和中间标准化参数在一定程度上缓解了这一问题,但仍然存在更深的网络比浅层网络具有更大的训练误差的问题。
基本结构
假设
多层的网络结构能够任意接近地拟合目标映射,那么也能任意接近地拟合其关于恒等映射的残差函数。记,则原来的目标映射表为。由此,可以设计如下结构。
残差单元
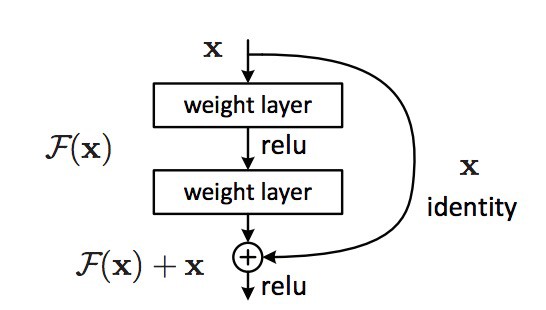
残差单元包含一条恒等映射的捷径,不会给原有的网络结构增添新的参数。
动机/启发
层数的加深会导致更大的训练误差,但只增加恒等映射层则一定不会使训练误差增加,而若多层网络块要拟合的映射与恒等映射十分类似时,加入的捷径便可方便的发挥作用。
实验
文章中列举了大量在ImagNet和CIFAR-10上的分类表现,效果很好,在此不表。
拾遗
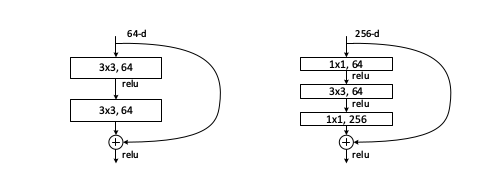
Deeper Bottleneck Architectures
两头的1 * 1巻积核先降维再升维,中间的3 * 3巻积核成为“瓶颈”,用于提取重要的特征。这样的结构跟恒等映射捷径配合,在ImageNet上有很好的分类效果。
Standard deviations of layer responses
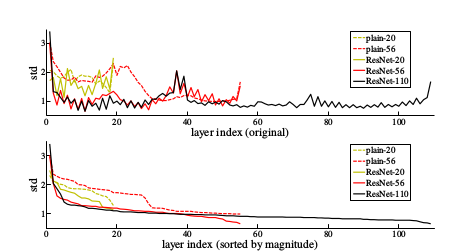
上图是在CIFAR-10数据集上训练的网络各层的相应方差(Batch-Normalization之后,激活之前)。可以看到,残差网络相对普通网络有更小的方差。这一结果支持了残差函数比非残差函数更接近于0的想法(即更接近恒等映射)。此外,还显示出网络越深,越倾向于保留流过的信息。
小结
深度残差网络在当年的比赛中几乎是满贯。
下面是我的一些(未经实验证实的)理解:
首先,其”跳级”的网络结构对深度网络的设计是一种启发,通过“跳级”,可以把之前网络的信息相对完整的跟后层网络结合起来,即低层次解耦得到的特征和高层次解耦得到的特征再组合。
再者,这种分叉的结构可以看作网络结构层面的”Dropout”: 如果被跳过的网络块不能习得更有用的信息,就被恒等映射跳过了。