权重衰减(weight dacay),即L^2范数惩罚,是最常见的正则化技术之一。本文将介绍它是如何起作用的。主要材料来自The Deep Learning Book。
为什么要引入权重衰减
机器学习的逻辑与我们最初解决问题的思维方式恰恰相反:要解决问题,一种经典的思路是把它拆成小问题,考虑之间的依赖,然后分而治之。而机器学习的哲学是“trail-error-correct”:先假设一堆可能的方案,根据结果去选择/调整这些方案,直到满意。换句话说,机器学习在假设空间中搜索最符合数据的模型:以果推因,即为最大似然的想法。随着数据量的增大,我们越来越需要表达能力更强的模型,而深度学习的优势正符合这一需要:通过分布式表示带来的指数增益,深度学习模型的扩展能力几乎是无限的(详见深度学习和分布式表示)。
有了模型(备选模型集),有了数据,就不得不面对机器学习领域的核心问题:如何保证模型能够描述数据(拟合)和生成数据(泛化)。
粗略来看,有以下三种情况:
- 我们假定的模型族不包含真实数据的生成过程:欠拟合/高偏差
- 匹配真实的数据生成过程
- 除了包含真实的生成过程,还包含了其他信息:过拟合/高方差
高偏差意味着我们的模型不够准确(模型族不足以描述数据),高方差意味着我们建模了不必要的信息(训练数据的随机性带来的)。前者通过提高模型的表述能力来解决(更深的网络),后者则需要合理的正则化技术来控制。这即是著名的trade-off。
深度学习模型的参数
对数据建模,其实是从数据中提取我们能够理解的信息。建立的模型,是从数据分布的空间到目标变量所在空间的映射。从这个角度看,我们通过模型带来的变换获得了数据的一种表示,我们认为能够理解和操作的表示。
为了表述这一变换,深度模型的套路是线性层施加变换,非线性层固定信息(不能平移),然后将这样的结构堆叠起来,分层提取数据特征。
这让我想起实变中证明定理的套路:先证明简单函数的情形,再推广到连续函数,再到勒贝格可积的函数。
常规的套路(MLP)在拟合普通的函数任务上能够胜任,但面对更复杂的图像等数据,就需要更灵活的网络结构。
非常出色的CNN, LSTM, Inception块, ResNet, DenseNet等结构,就是加入了人类的先验知识,使之更有效的提取图像/音频数据分布空间的特征。(所以Manning有次在课堂上说,机器学习事实上还是人类在学习:机器只是在求导数、做乘法,最好的模型都是人们学习出来的。)
人们确实设计了很多巧妙的结构来解决不同的问题,但落实到网络的层和单元上,仍是最基本的矩阵乘法、加法运算。决定模型表述能力的,也正是这些普通的乘法运算中涉及的矩阵和向量了。
权重衰减如何起作用
下面我们通过观察加入权重衰减后目标函数的梯度变化来讨论权重衰减是如何起作用的。可以跳过公式部分直接看最后一段。
————————————推导部分—————————
简单起见,令偏置为0,模型的目标函数:
$$J_{1}(w; X,y)=\frac{\alpha}{2} w^T w+J(w; X,y)$$
对应的梯度为:
$${\nabla}{w} J{1}(w; X,y) = \alpha w + {\nabla}_{w} J(w; X,y)$$
进行梯度下降,参数的更新规则为:
$$w = w - \epsilon (\alpha w + {\nabla}_{w} J(w; X,y)) $$
也就是:
$$w = (1 - \epsilon \alpha )w - \epsilon {\nabla}_{w} J(w; X,y)$$
从上式可以发现,加入权重衰减后,先对参数进行伸缩,再沿梯度下降。下面令 $x^{(1)}$ 为使目标函数达到最优的参数值,在其附近考虑目标函数的二次近似:
$$J(w) \approx J(w^{(1)}) + \frac{1}{2} (w - w^{(1)})^T H (w - w^{(1)})$$
其中 $H$ 为近似目标函数在的Hessian矩阵。当近似目标函数最小时,其梯度为 $0$ ,即:
$${\nabla}_{w} J(w) \approx H(w - w^{(1)})$$
该式也向我们说明了基于梯度的优化算法主要的信息来自Hessian矩阵。添加入权重衰减项之后,上式变为(记此时的最优点为 $w^{(2)}$ ):
$${\nabla}{w} J{1}(w) \approx \alpha w^{(2)} + H(w^{(2)} - w^{(1)}) = 0$$
所以
$$w^{(2)} = (H + \alpha I)^{-1} H w^{(1)} $$
该式表明了了加入正则化对参数最优质点的影响,由Hessian矩阵和正则化系数 $\alpha$ 共同决定。
进一步将Hessian矩阵分解,可以得到:
$$w^{(2)} = Q(\Lambda + \alpha I)^{-1} \Lambda Q^T w^{(1)}$$
其中, $Q$ 为正交矩阵,$\Lambda$ 为对角矩阵。这样可以看到,权重衰减的效果是沿着由 $H$ 的特征向量所定义的轴缩放 $w$, 具体的伸缩因子为 ${\frac{ {\lambda}_{i} }{ {\lambda}i + \alpha }}$ ,其中 ${\lambda}{i}$ 表示第 $i$ 个特征向量对应的特征值。
当特征值 $\lambda$很大(相比 $\alpha$)时,缩放因子对权重影响较小,因而更新过程中产生的变化也不大;而当特征值较小时, $\alpha$的缩放作用就显现出来,将这个方向的权重衰减到0。
这种效果也可以由下图表示:
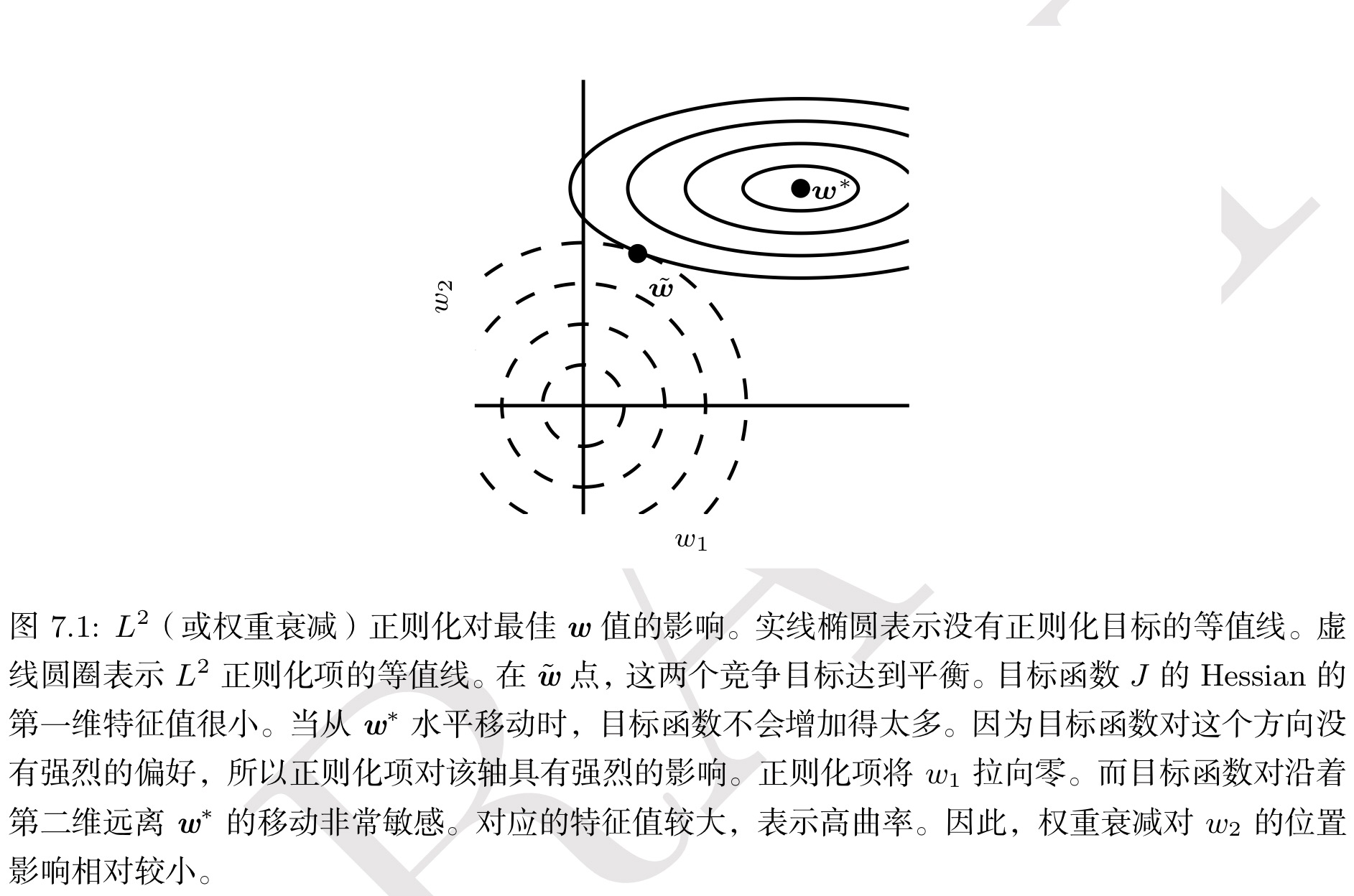
———————————————————推导部分结束———————————————————
总结来说,目标函数的Hessian矩阵(显式、隐式或者近似的)是现有优化算法进行寻优的主要依据。通过控制权重衰减的 $\alpha$ 参数,我们实际上控制的是在Hessian矩阵的特征方向上以多大的幅度缩放权重,相对重要(能够显著减小目标函数)的方向上权重保留比较完好,而无助于目标函数减小的方向上权重在训练过程中逐渐地衰减掉了。而这也就是权重衰减的意义。
从宏观上来看,对目标函数来说,特征值较大的方向包含更多有关数据的信息,较小的方向则有随机性的噪声,权重衰减正是通过忽略较少信息方向的变化来对抗过拟合的。
$L^1$ 范数正则化
通过类似的推导,可以得到加入了 $L^1$ 范数惩罚项对参数最优解的影响如下:
$$w^{(2)}{i} = sign(w^{(1)}{i}) max \big{|w^{(1)}{i}| - \frac{\alpha}{H{i,i}}, 0 \big}$$
相比 $L^2$ 范数的影响,这是一个离散的结果,因而 $L^1$ 范数惩罚会将参数推向更加稀疏的解。这种稀疏性质常被用作特征选择。
权重衰减的贝叶斯解释
在贝叶斯统计的框架下,常用的推断策略是最大后验点估计(Maximum A Posteriori, MAP)。有如下的推断公式(由贝叶斯定律导出):
$${\theta}_{MAP} = argmax p(\theta | x) = argmax (log p( x | \theta) + log p(\theta))$$
上式右边第一项是标准的对数似然项,而第二项对应着先验分布。
在这样的视角下,我们只进行最大似然估计是不够的,还要考虑先验 $p(\theta)$ 的分布。而当假定参数为正态分布 $N(w; 0, \frac{1}{\lambda}I^2)$ 时,带入上式( $\theta$ 为参数),即可发现第二项的结果正比于权重衰减惩罚项 $\lambda w^T w$ ,加上一个不依赖于 $w$ 也不影响学习过程的项。于是,具有高斯先验权重的MAP贝叶斯推断对应着权重衰减。
权重衰减与提前终止
提前终止也是一种正则化技术,其想法简单粗暴:每个epoch之后在验证集上评估结果,当验证集误差不再下降的时候,我们认为模型已经尽它所能了,于是终止训练过程。
提前终止以牺牲一部分训练数据来作为验证数据来的代价来对抗过拟合,其逻辑是实证主义的。
然而,在二次近似和简单梯度下降的情形下,可以观察到提前终止可以有相当于权重衰减的效果。
我们仍考虑目标函数的二次近似:
$$J(w) \approx J(w^{(1)}) + \frac{1}{2} (w - w^{(1)})^T H (w - w^{(1)})$$
记最优参数点为 $w^{(1)}$ ,其梯度为:
$${\nabla}_{w} J(w) \approx H(w - w^{(1)})$$
不加入正则化项,其梯度下降的更新策略(从第 $\tau-1$ 步到 $\tau$ 步)为:
$$ w^{(\tau)} = w^{\tau - 1)} - \epsilon H (w^{(\tau - 1)} - w^{(1)})$$
累加得到
$$ w^{(\tau)} - w^{(1)} = (I - \epsilon H) (w^{(\tau - 1)} - w^{(1)})$$
将Hessian矩阵分解,得到如下形式
$$ w^{(\tau)} = Q[I - (I - \epsilon \Lambda) ^ {\tau}] Q^T w^{(1)} $$
将加入正则化项的权重影响改写为
$$ w^{(2)} = Q[I - (\Lambda + \alpha I) ^ {-1} \alpha] Q^T w^{(1)} $$
对比可以得到,如果超参数 $\epsilon, \alpha, \tau$ 满足
$$ (I - \epsilon \Lambda) ^ {\tau} = (\Lambda + \alpha I) ^ {-1} \alpha $$
则提前终止将与权重衰减有相当的效果。具体的,即第 $\tau$ 步结束的训练过程将到达超参数为 $\alpha$ 的 $L^2$ 正则化得到的最优点。
但提前终止带来的好处是,我们不再需要去找合适的超参数 $\alpha$ ,而只需要制定合理的终止策略(如3个epoch均不带来验证集误差的减小即终止训练),在训练成本的节约上,还是很值得的。