本文是MobileNets的第二版。第一版中,MobileNets全面应用了Depth-wise Seperable Convolution并提出两个超参来控制网络容量,在保持移动端可接受的模型复杂性的基础上达到了相当的精度。而第二版中,MobileNets应用了新的单元:Inverted residual with linear bottleneck,主要的改动是添加了线性Bottleneck和将skip-connection转移到低维bottleneck层。
Intuition
本篇比较丰富的地方是对网络中bottleneck结构的探讨。
在最早的Network in Network工作中,1x1卷积被作为一个降维的操作而引入,后来逐渐发展为Depth-wise Seperable Convolution(可分离卷积)并被广泛应用,堪称跟skip-connection同样具有影响力的网络部件。在Inception单元最初提出之时,具有较多channel的feature map被认为是可供压缩的,作者引入1x1卷积将它们映射到低维(较少channel数)空间上并添加多路径处理的范式。之后的Xception、MobileNets等工作则将可分离卷积应用到极致:前者指出可分离卷积背后的假设是跨channel相关性和跨spatial相关性的解耦,后者则利用可控的两个超参来获得在效率和精度上取得较好平衡的网络。
文中,经过激活层后的张量被称为兴趣流形,具有维HxWxD,其中D即为通常意义的channel数,部分文章也将其称为网络的宽度(width)。
根据之前的研究,兴趣流形可能仅分布在激活空间的一个低维子空间里,利用这一点很容易使用1x1卷积将张量降维(即MobileNet V1的工作),但由于ReLU的存在,这种降维实际上会损失较多的信息。下图是一个例子。

上图中,利用MxN的矩阵B将张量(2D,即N=2)变换到M维的空间中,通过ReLUctant后(y=ReLU(Bx)),再用此矩阵之逆恢复原来的张量。可以看到,当M较小时,恢复后的张量坍缩严重,M较大时则恢复较好。
这意味着,在较低维度的张量表示(兴趣流形)上进行ReLU等线性变换会有很大的信息损耗。因而本文提出使用线性变换替代Bottleneck的激活层,而在需要激活的卷积层中,使用较大的M使张量在进行激活前先扩张,整个单元的输入输出是低维张量,而中间的层则用较高维的张量。文中所用单元的演化过程如下:
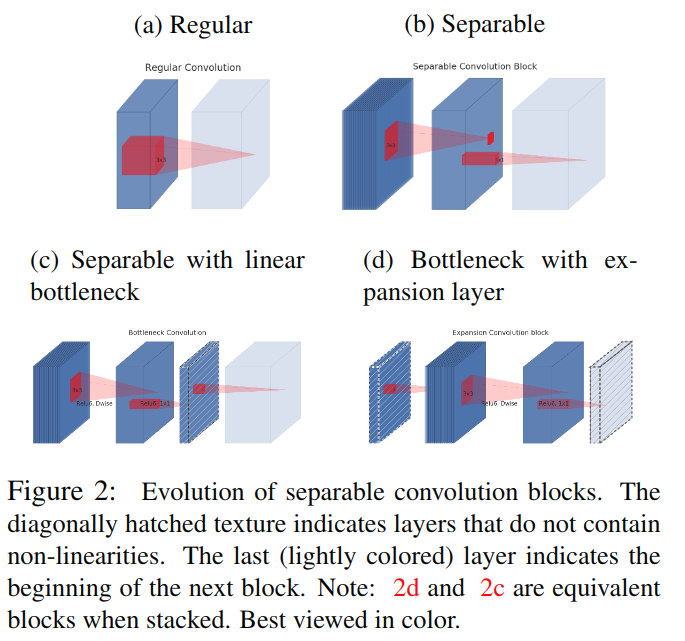
。图a中普通卷积将channel和spatial的信息同时进行映射,参数量较大;图b为可分离卷积,解耦了channel和spatial,化乘法为加法,有一定比例的参数节省;图c中进行可分离卷积后又添加了bottleneck,映射到低维空间中;图d则是从低维空间开始,进行可分离卷积时扩张到较高的维度(前后维度之比被称为expansion factor,扩张系数),之后再通过1x1卷积降到原始维度。
实际上,图c和图d的结构在堆叠时是等价的,只是观察起点的不同。但基于兴趣流形应该分布在一个低维子空间上的假设,这引出了文章的第二个关键点:将skip-connection转移到低维表达间,即Inverted residual block。
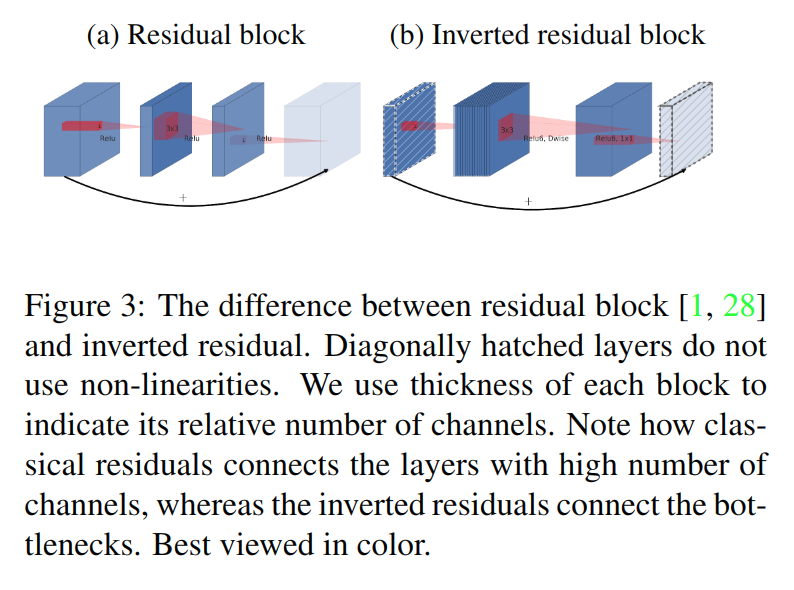
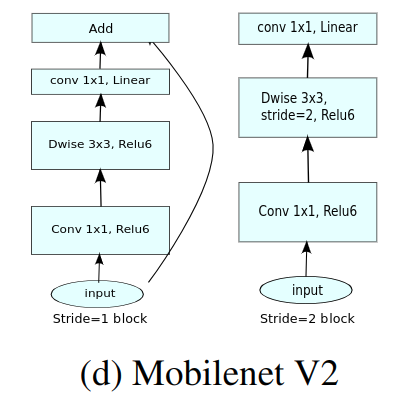
综合以上两点,文章中网络所用的基本单元如下:

文章指出,这种设计将层输入、输出空间跟层变换分离,即网络容量(capacity)和表达力(expressIveness)的解耦。
Experiments
MobileNet V2的整体结构如下表:

上图中,t代表单元的扩张系数,c代表channel数,n为单元重复个数,s为stride数。可见,网络整体上遵循了重复相同单元和加深则变宽等设计范式。也不免有人工设计的成分(如28^2*64单元的stride,单元重复数等)。
ImageNet Classification
MoblieNets V2仍然集成了V1版本的两个超参数,在ImageNet上的实验结果如下:
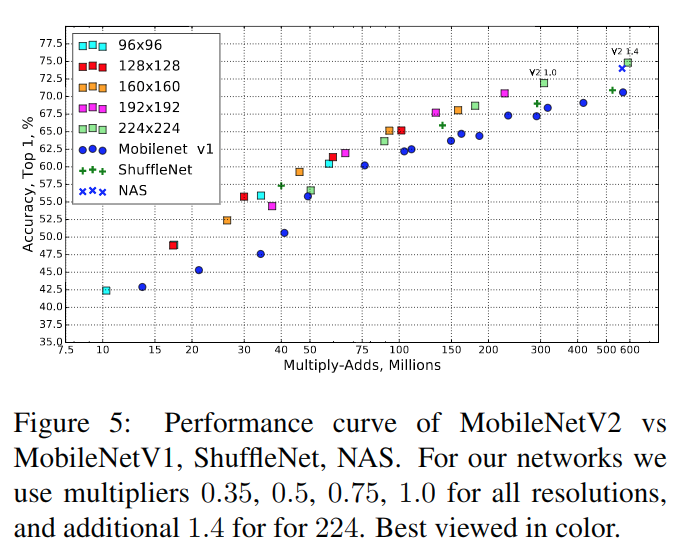
可以看到相比V1版本优势明显,在精度方面跟NAS搜索出的结构有相当的表现。
Object Detection
文章还提出SSDLite来更好适应移动端需求,改动是将head部分的普通卷积都替换为了可分离卷积。
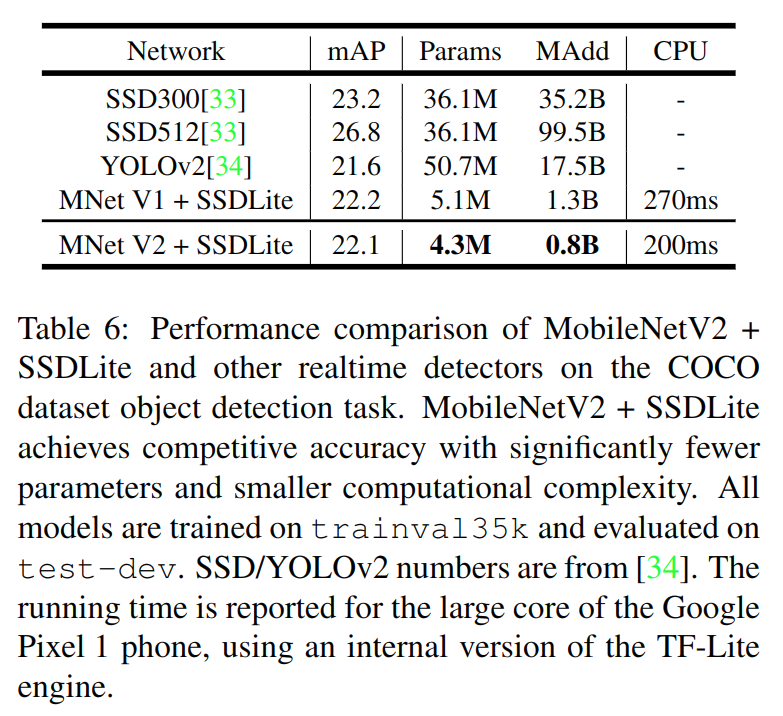
上面是在COCO上的表现,可以看到精度方面跟YOLOv2和SSD300相当(尽管很低,相比SOTA差距还很大),但模型参数和运算复杂度都有一个数量级的减少。最后的CPU时间是在Pixel上测得,可以到5FPS,达不到真正移动实时的要求,但也是不小的推进了(并没有给出GPU上的推断时间,而Pixel+TF-Lite的benchmark又跟其他网络难以产生有效的比较)。
Segmentation
下图是在VOC上分割的结果:
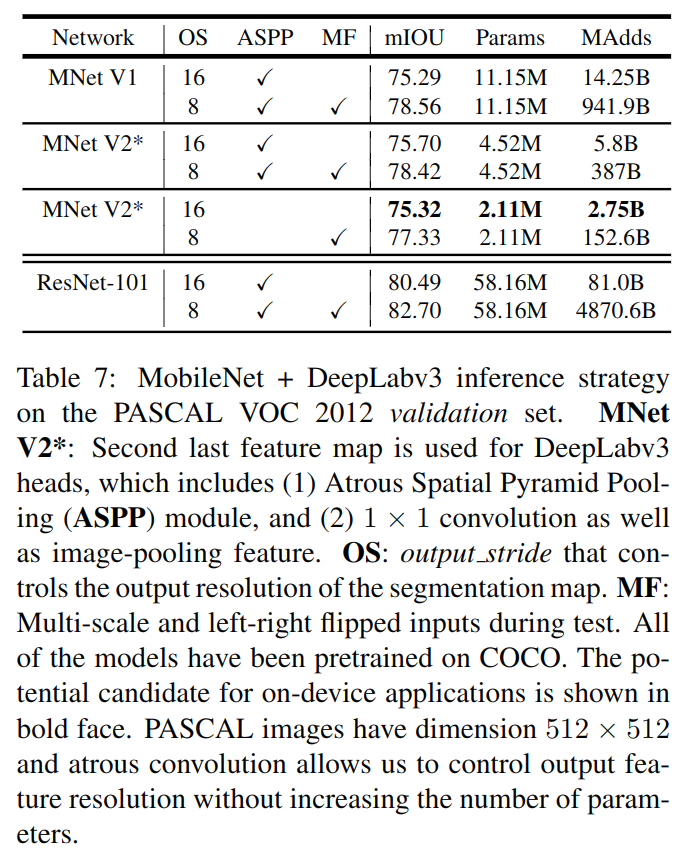
Ablation Study
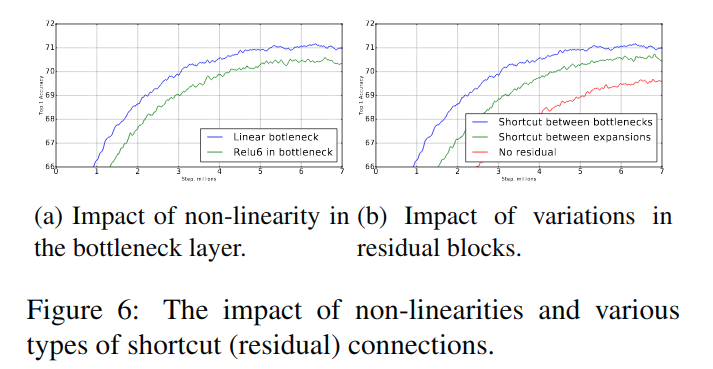
文章还做了关于线性变换bottleneck替代ReLU和skip-connection位置的实验,进一步支撑之前的分析。
附录
本篇文章的附录部分提供了紧的n维流形在经过升维线性变化加ReLU后被映射到子集的期望大小的界,这个界说明在扩张到足够高的维度后,升维线性变换加ReLu能以较高的概率可逆(保持信息)并加入非线性。
上面的结论是非常拗口的。自己的理解是,使用ReLU引入非线性的同时会导致信息损失(非线性指不会被卷积、全连接等线性映射吸收掉,信息损失则是指ReLU将<0的输入置0,输入变得稀疏,而若所有输入的某一维度都被置0,则会使输入空间本身降维),我们要对抗这一可能的信息损失,需要将输入先扩张,即y=ReLU(Bx),x为R^n空间上的输入,B为m×n矩阵,我们期望m足够大,以达到扩张的效果并在经过ReLU后保持y跟x的信息量同样多(文中的引理二,即是证此变换可逆性的一个条件,应该是借用了代数的概念,矩阵在经过可逆变换后不会降秩,秩成为衡量信息损失的指标)。
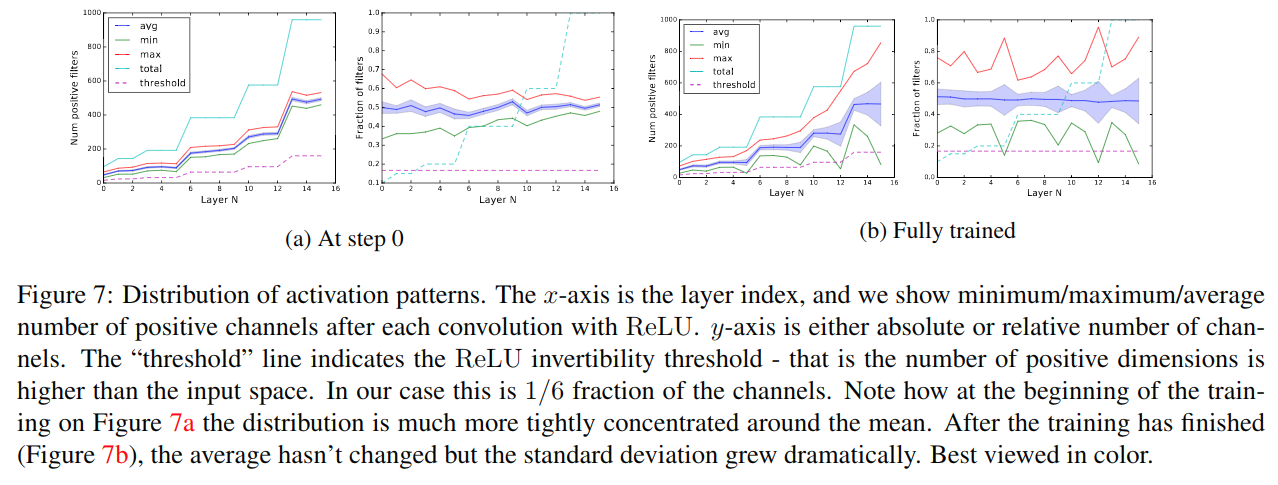
在ReLU(Bx)算符可逆性的问题上,作者做了一些经验性实验,如上图。a和b分别为训练前后,每层正激活channel数(可逆性条件)和其占总channel数比例的分布。图a和图b的左图,随网络加深,channel数增多,即变宽;训练前后,方差增大,且有两层低于了可逆性条件阈值(图b左图中绿色线低于紫色阈值的部分)。右图是一个比例,由于随机初始化,均值在0.5附近,训练后同样方差增大,而可逆性条件阈值一直为1/6(即为MobileNet V2扩张系数的倒数)。
附录的Theorem 1则证明了ReLU(Bx)算符将输入x压缩后的空间维度(n-volume)的界,此界在扩张系数较大时可以跟原空间相当,即信息损失很小。
小结
能够看到附录里给出文中假定或观察的数学证明的论文还是开心的。太多论文只是终于实验的SOTA而避而不谈Insights,况且给出证明。尽管本篇附录中的证明仍有经验主义的部分,且并没有完全定义清楚问题和结论,其对后续工作的启发价值还是有的。
这也暴露了当前领域的通病,我们没有共通的一套语言来描述自己的网络,譬如,如何定义网络的容量、表达力,如何衡量信息的损失。没有通用的定义造成了论文表述常常有令经验少者难以理解的表达。去定义这样一套语言和标准来为网络设计提供参考,希望成为以后的研究热点,也是我自己的一个思考方向。
总体来看,本篇文章提供的两点改进都是有启发性的,但并不完整,需要更多工作来补充。另外源码没有给出,会尝试复现。