本文的两个主要参考资料:
- Yoshua Bengio在2016年九月Deep Learning School的演讲Foundations and Challenges of Deep Learning。YouTube
- Deep Learning, Goodfellow et al, Section 15.4
从机器学习到人工智能
在演讲中,Bengio提到从机器学习到人工智能有五个关键的飞跃:
- Lots of data
- Very flexible models
- Enough computing power
- Powerful priors that can defeat the curse of dimensionality
- Computationally efficient inference
第一点已经发生,到处都提大数据,到处都在招数据分析师。
我在读高中时,就曾预感数据将是新时代的石油和煤炭,因为数据正是人类社会经验的总结,数据带来的知识和见解将在驱动社会进步中发挥越来越重要的作用,而自己要立志成为新时代的矿工。
第二点在我看来有两个例子,一是核技巧,通过核函数对分布空间的转换,赋予了模型更强大的表述能力;二是深度神经网络,多层的框架和非线性的引入使得模型理论上可以拟合任意函数。
第三点,借云计算的浪潮,计算力不再是一项资产而是一项可供消费的服务,我们学生也可以廉价地接触到根本负担不起的计算力资源。而GPU等芯片技术的进步也为AI的浩浩征程添砖加瓦。
第五点,近期发布的Tensorflow Lite和Caffe2等工具也有助于越来越多地将计算任务分配在终端上进行,而非作为一个发送与接收器。
最后第四点,也是这篇文章的中心话题:借助分布式表示的强大能力,深度学习正尝试解决维度带来的灾难。
没有免费的午餐
简单说,没有免费的午餐定理指出找不到一个在任何问题上都表现最优的模型/算法。不同的模型都有其擅长的问题,这由该模型建立时引入的先验知识决定。
那么,深度学习加入的先验知识是什么?
Bengio用的词是Compositionality,即复合性,某一概念之意义由其组成部分的意义以及组合规则决定。复合性的原则可以用于高效地描述我们的世界,而深度学习模型中隐藏的层正是去学习其组成部分,网络的结构则代表了组合规则。这正是深度学习模型潜在的信念。
分布式表示带来的指数增益
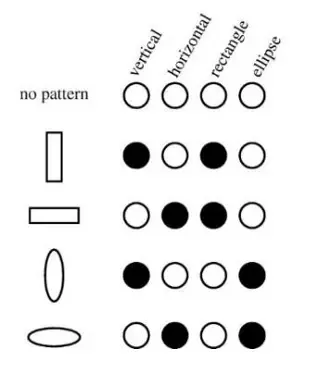
分布式表示(Distributed Representation)是连接主义的核心概念,与复合性的原理相合。整体由组成它的个体及其组合来表示。请看下面的例子:
描述一个形状,我们将其分解为不同的特征来表述。分布式表示是一种解耦,它试图复杂的概念分离成独立的部分。而这也引出了分布式表示带来的缺点:隐藏层学到的分解特征难以得到显式的解释。
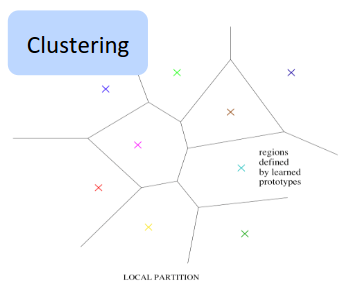
传统的机器学习算法,如K-Means聚类、决策树等,大多使用的是非分布式表示,即用特定的参数去描述特定的区域。如K-Means聚类,我们要划分多少区域,就需要有多少个中心点。因而,这类算法的特点是,随着参数个数的提升,其能描述的概念线性增长。
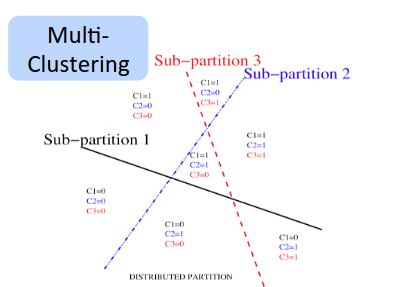
使用分布式表示的深度网络,则可以享受到指数级的增益,即,随着参数个数的提升,其表述能力是指数级的增长。具有个值的个特征,可以描述个不同的概念。
分布式表示在泛化上的优势
分布式的想法还可以得到额外的泛化优势。通过重新组合在原有数据中抽离出来的特征,可以表示得到原有数据中不存在的实例。在Radford et al.的工作中,生成模型区习得了性别,并能从“戴眼镜的男人”-“男人”+“女人”=“戴眼镜的女人”这样的抽象概念表达式中生成实例。
分布式表示与巻积神经网络
巻积神经网络不同的滤波器习得的特征可以为分布式表示的概念分解这一特性提供一些例子。下图是VGG16不同滤波器得到结果的可视化表示,
出自Francois Chollet的博文How convolutional neural networks see the world
可以看到,浅层的滤波器学到的是简单的颜色、线条走向等特征,较深的滤波器学到复杂的纹理。
量子计算机与分布式表示
在我看来,量子计算机的激动人心之处也在于其表示能力。一个量子态可以表示原先两个静态表示的信息,原先需要8个单位静态存储表示的信息只需要3个量子态单位即可表示,这也是指数级的增益。在这一点上,计算模型和概念模型已然殊途同归。
小结
从经验中总结原则,用原则生成套路,正是我们自己处理和解决新问题的途径。通过解耦得到的信息来消除未知和不确定性,是我们智能的一部分。我们眼中的世界,只是适合我们的一种表示而已。也许,真正的人工智能到来那一刻,会是我们创造的机器“理解”了自己的表示系统之时——我们所关注的可解释性,也就无关紧要了。